Large Ensemble model simulations help to better quantify sources of uncertainty in climate projections
Climate projections contain uncertainty. Quantifying and understanding this uncertainty is important not only for scientific interpretation and guiding climate model development, but also for science communication. Climate projection uncertainty is typically split into three sources: model uncertainty, internal variability, and scenario uncertainty – or in other words: uncertainty due to our lack of understanding or lack of agreement among different models, irreducible climate noise, and unknown future human decisions on greenhouse gas emissions.
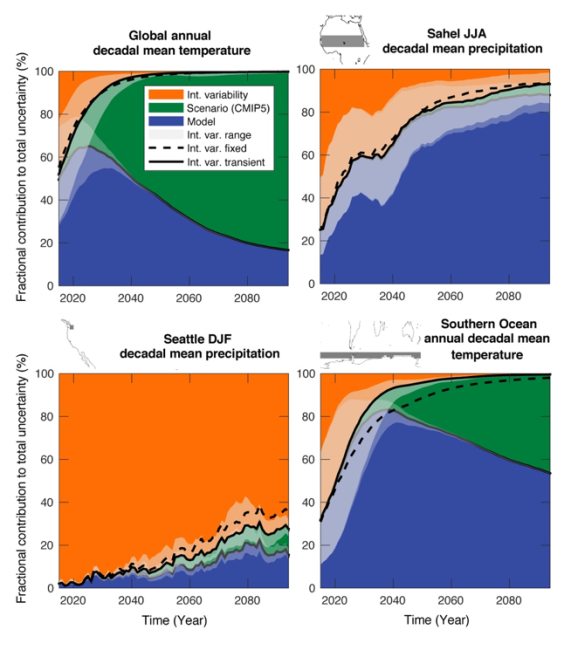
Figure 1. Sources of uncertainty in climate projections and their relative importance for different variables, regions and seasons. The solid black lines indicate the borders between sources of uncertainty; the transparent white shading around those lines is the range of this estimate based on different SMILEs. In other words, when the white shading is large, the models disagree on how large internal variability actually is. The dashed line marks the dividing line if internal variability is assumed to stay fixed at its 1950–2014 multi-SMILE mean. In other words, when there is a noticeable difference between the dashed and solid black line, a forced change to internal variability is detectable (click image to enlarge).
Here, we revisit the Hawkins&Sutton paper from 2009 on uncertainty partitioning to see how robust the method and results are in light of a new generation of models and in particular a new collection of single model initial-condition large ensembles (SMILEs). The method relies on being able to separate climate change projections into an anthropogenically-forced response component and a noise component related to internal variability. Historically, with only few simulations available per model, this was done via a 4th order polynomial fit to the model projections (representing the forced response) and its residual (representing internal variability). However, these statistical assumptions are likely to conflate internal variability with the forced response in cases where there exists relatively large low-frequency (decadal-to-multidecadal) internal variability.
With the advent of multiple SMILEs, these statistical assumptions can be tested, as the SMILEs allow a cleaner separation between sources of uncertainty. For globally-averaged quantities such as temperature and precipitation, the original method is shown to work well and a consistent picture emerges irrespective of whether the SMILEs, CMIP5 or CMIP6 is used. Specifically, internal variability is important at the beginning of each projection horizon (say, over the next 1-2 decades), after which model uncertainty becomes dominant. Further into the future, scenario uncertainty becomes increasingly important. However, this picture can vary depending on which region of the globe and which climate variable is considered.
Using SMILEs, the potential method bias from using a 4th order polynomial fit to estimate the forced response can be calculated. For global temperature this is small, but at regional scales or for variables with a lot of internal variability, the potential bias can be substantial. Luckily, this bias can be greatly reduced with SMILEs.
Comparing different model generations, model uncertainty in global temperature was found to be larger in CMIP6 than in CMIP5, but we show that this is mostly due to the wider range of climate sensitivity in CMIP6. In fact, because models that warm a lot in the future tend to also warm too much over the historical period, we can apply an observational constraint to the models and bring the two model generations into better agreement.
The SMILEs also enable, for the first time, to confidently calculate model differences in the magnitude of internal variability itself, as well as determine whether we should expect the internal variability to change with climate change (see Figure 1). Our analysis revealed sizable differences between models’ internal variability, illustrating the need for observational constraints on simulated variability – not just mean and trend, which are more traditional foci of model evaluation. At the same time, models often agree on the projected forced changes in variability, such as increases in precipitation variability or decreases in temperature variability in certain regions, lending confidence to those results.
Overall, this study demonstrates the added value of a collection of SMILEs for quantifying and diagnosing uncertainty in climate projections, an endeavor that will continue into the foreseeable future as we try to improve the reliability of climate projections.
Partitioning climate projection uncertainty with multiple large ensembles and CMIP5/6 (Earth System Dynamics)
Topics
- Modeling
- Climate Change
